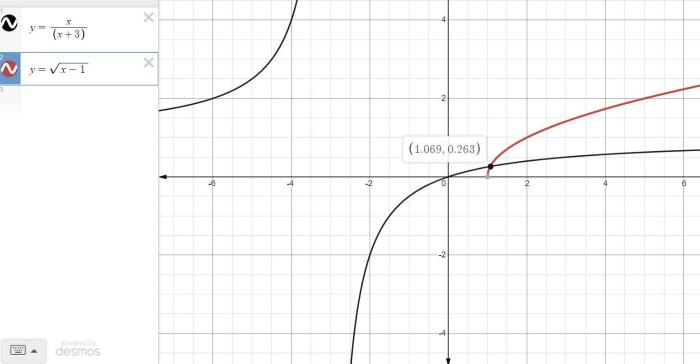
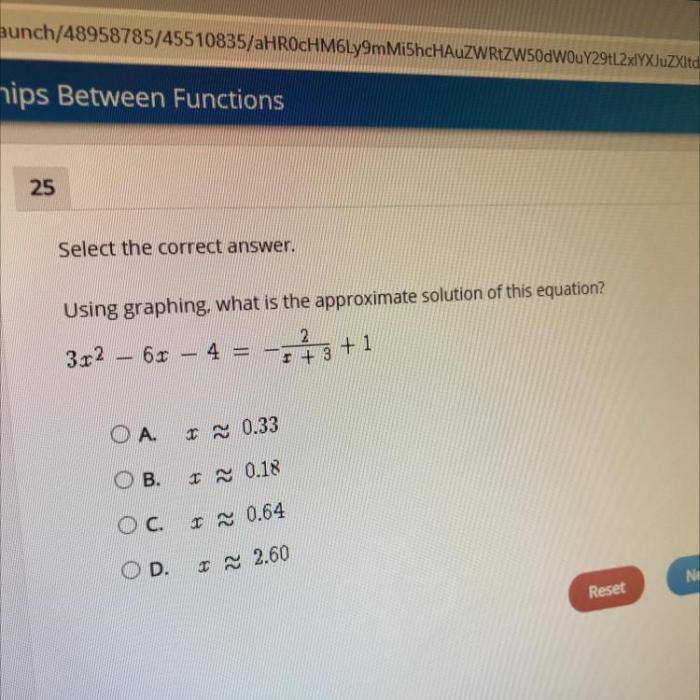
Using graphing what is the approximate solution of this equation – Using graphing to approximate the solution of an equation offers a powerful tool for tackling complex mathematical problems. This engaging exploration delves into the intricacies of graphing techniques, unlocking the secrets of finding approximate solutions with precision and efficiency.
As we embark on this journey, we will uncover the diverse graphing methods available, unraveling their strengths and applications. We will delve into the types of equations that yield to the power of graphing, dissecting their unique characteristics that make them amenable to this approach.
Graphing Techniques to Approximate Equation Solutions
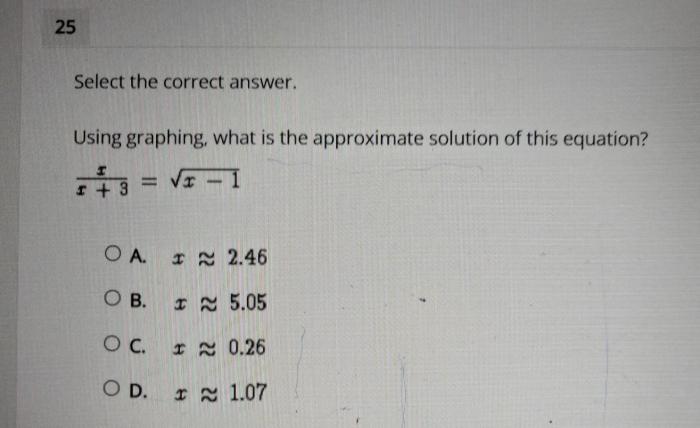
Graphing techniques offer a visual approach to approximating solutions of equations. By plotting the equation’s graph and analyzing its behavior, one can estimate the values of the variables that satisfy the equation.
Types of Graphing Techniques
- Point Plotting:Manually plotting points on the graph based on the equation’s values.
- Slope-Intercept Method:Using the slope and y-intercept to sketch the graph.
- Intercepts Method:Finding the x- and y-intercepts to determine the graph’s position.
- Table of Values:Creating a table of input and output values to visualize the graph.
Types of Equations, Using graphing what is the approximate solution of this equation
Graphing techniques are applicable to various equation types:
- Linear Equations:Equations of the form y = mx + b, where m is the slope and b is the y-intercept.
- Quadratic Equations:Equations of the form ax 2+ bx + c = 0, where a, b, and c are constants.
- Polynomial Equations:Equations of the form a nx n+ a n-1x n-1+ … + a 1x + a 0= 0, where a n≠ 0.
Graphing Software
Graphing software simplifies the graphing process and provides additional features:
- Desmos:Online graphing calculator with advanced functions and customization options.
- GeoGebra:Interactive geometry and algebra software with 3D graphing capabilities.
- MATLAB:Professional-grade mathematical software with powerful graphing and data analysis tools.
Accuracy and Limitations
Graphing approximations have limitations:
- Accuracy:Approximations can be less precise than analytical methods.
- Ambiguity:Graphs may not provide unique solutions, especially for complex equations.
- Non-visual Equations:Graphing is not applicable to equations that cannot be expressed graphically.
Examples and Applications
| Equation Type | Graphing Technique | Solution Accuracy | Application |
|---|---|---|---|
| Linear | Slope-Intercept Method | High | Linear regression, data analysis |
| Quadratic | Intercepts Method | Moderate | Projectile motion, parabolic curves |
| Polynomial | Point Plotting | Low | Approximating roots of polynomials |
Essential FAQs: Using Graphing What Is The Approximate Solution Of This Equation
What types of equations are suitable for graphing techniques?
Graphing techniques are particularly effective for solving linear, quadratic, polynomial, and exponential equations.
How can I improve the accuracy of my graphing approximations?
To enhance accuracy, use a graphing calculator or software, zoom in on the relevant section of the graph, and consider the scale and units of the axes.